The TI-Nspire non-CAS can evaluate rational expressions and display graphs of rational functions. Unfortunately, it cannot algebraically simplify rational expressions.
Let's take a look at how the calculator can help our work with rationals.
Example
1:
Given:
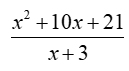
a) Evaluate the expression at x = 5.
Ans: 12
First, store 5 in the x-variable.
The calculator can find, or verify, the substitution for evaluating this expression.
b) Determine the domain of the expression.
Ans: All reals except x = -3.
First, store a possible troublesome value
(such as -3) in the x-variable.
The calculator can verify whether a value you pick creates a zero denominator, by stating that the answer is "undefined" (undef).
|
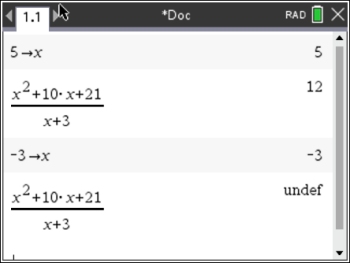
a) The calculator shows that when 5 is substituted into the rational expression, the result is 12.
b) The calculator shows that our choice of x = -3
is a trouble spot. That choice creates a zero denominator causing the rational expression
to be undefined.
|
c) For what value of x will this expression equal zero?
Ans. x = -7
If the expression equals zero, then its graph will cross the x-axis at that value.
Algebraically: 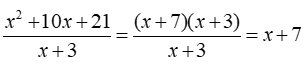
The expression equals zero at x = -7 as the numerator equals 0, but the denominator does not equal zero.
But, at x = -3 while this value makes the numerator zero, it also makes the denominator 0, or undefined. So, x = -3 is not an option.
|
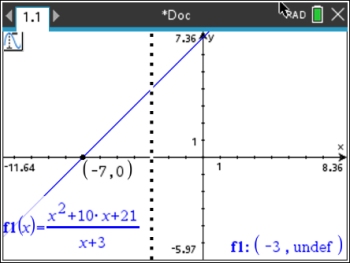
c) The TRACE command created the vertical
dotted line and produced the label in the lower
right corner
(-3, undef).
This indicates a "hole" in the graph
at x = -3. (See Rational Graphs for more details).
|

|
Example
2:
Given:
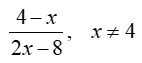
This expression is equivalent to which choice:
1) ½ 2) -½ 3) ¼ 4) -¼
Ans. Choice 2
This type of problem can be tricky to factor as it involves factoring out a negative one.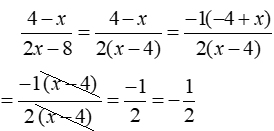
So, using our calculator for checking can verify that we did not make a mistake in our factoring. |

First, store a value (not 4) in the x-variable.
Setting the rational expression EQUAL to one of the equivalent choices will indicate whether that choice is correct ("true"). From our first "check", we see that Choice 1) ½ is not the correct choice.
But Choice 2) -½ is the correct choice.
|

|
|

