|

Trigonometry Formulas for Area of Triangle
and Area of Parallelogram
The formula for the
area of a triangle is

where b stands for the base and h stands for the altitude
(height)
drawn to that base. |
|
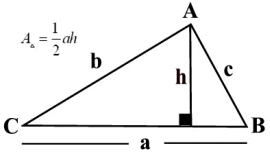
(lettering the diagram is of no importance to the
formula) |
|
By using trigonometry in the right triangle (on the left
side of the diagram), we find:
|
|
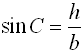
Multiplying by b, gives 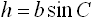 . .
Substituting this new value of h into the area formula gives the trig area of
triangle formula:
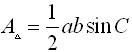 |
|
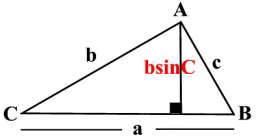
SAS Formula
for the area of a triangle
where the pattern is to use "two sides and
the sine of the included angle".
|
The diagonal of a parallelogram
divides the parallelogram into two congruent triangles.
Consequently, the area of a parallelogram can be thought of as
doubling the area of one of the triangles formed by a diagonal.
This gives the trig area formula for a
parallelogram:
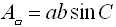 |
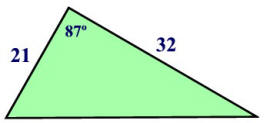
Example 1:
| Given the triangle at
the right, find its area, to the nearest hundredth.
|
 |
|
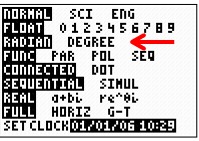
Be careful!!! When using your graphing calculator, be
sure that you are in DEGREE Mode,
or that you are using the degree symbol
if in RADIAN Mode. |
|
Degree Mode: |
 |

|
|
Radian Mode:
Find degree symbol under
ANGLE (2nd APPS) |
 |
 |
|
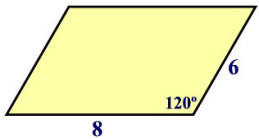
Example 2:
Given the parallelogram
at the right, find its area to the nearest hundredth.
|
Again!!! Be
sure that you are in DEGREE Mode,
or that you are using the degree symbol
if in RADIAN Mode. |
If this problem had asked for an
EXACT answer, do not
use your calculator, as the calculator rounds the value for sin
120º.
It will be necessary to use the 30º- 60º- 90º
reference triangle in Quadrant II. The EXACT ANSWER will
be
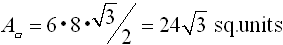
|
Check to see that the exact answer
yields the calculator decimal answer. |
 |
|
|
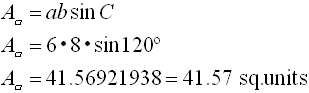

|

Finding Your Way Around
TABLE of CONTENTS
|